公認心理師・臨床心理士・心理職(心理系公務員)を目指す方々のための「心理学用語」を説明したサイトです
心理学用語集: 正規分布・標準得点・偏差値
6 - 統計・研究法 > 統計 > 13- 正規分布・標準得点・偏差値
統計にとって欠かせない用語が、「正規分布」です。ここでは、正規分布と標準偏差の関連や、標準得点・偏差値についてまとめます
用語:
正規分布
正規分布とは、「連続的な変数に関する平均値の付近に集積するようなデータがとる確率分布」のことです。つりがね状の形をしています。
確率分布とは、そのデータの値が現れる確率を表しています。
確率分布の具体例)
数学のテストを210人が受けたとします。10人は得点20点だった場合、20点の生じた確率は10人÷210人=約5%となります。
点数を取った人数が下図の棒グラフとすると、それらに対応した確率分布図は「50点」を頂点としたつりがね状の形となります。
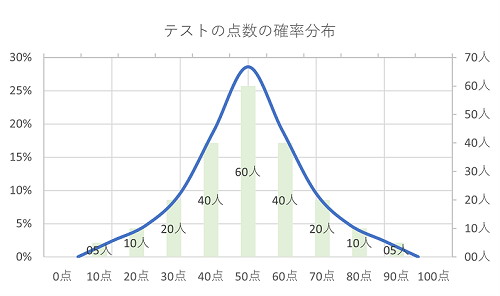
あるデータ値が多数の独立した因子(要因)の和として表される確率分布は、正規分布に従う事がわかっています。
したがって、心理学で扱われるデータの値(例:知能など)の多くは、正規分布に従うことを前提として扱われています。
また、統計において「中心極限定理」も前提となります。中心極限定理とは、いかなる分布からの標本であっても「その平均値の分布」は、母集団の平均と分散をもつ正規分布に近づくというものです。
正規分布の標準偏差:
データの分布が、正規分布に従う場合、標準偏差SDとデータ分布には下記の関係があります。
- 平均値を中心として、「±1SD (標準偏差)」以内のデータは、約68%が含まれている
(平均値プラス1SD以内に約34%、平均値マイナス1SD以内に約34%) - 平均値を中心として、「±2SD (標準偏差)」以内のデータは、約95%が含まれている
(平均値プラス2SD以内に約47.5%、平均値マイナス1SD以内に約47.5%)
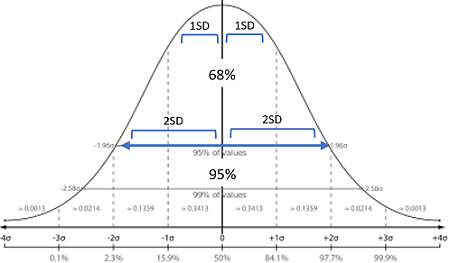
これらの特徴から、正規分布にしたがうデータの値が分布のどのあたりに位置しているかがわかります(上位何%、下位何%)。
例)国語の小テストの平均点が50点、標準偏差SDが20点とします。
「平均点±2SD」=「10点〜90点」の点数を取る人は、約95%いるということになります。
逆に、「0点〜9点」と「91点〜100点」をとった人は、100%-95% = 5% となります。
したがって、5%の半分の下位2.5%の人は9点以下であり、上位2.5%の人は91点以上となります。
尖度と歪度:
尖度(せんど)とは、確率分布のとがり度合いを表す指標です。
正規分布は、尖度が0または3に定義されています。
尖度が大きいほど、鋭い形(細長い形)であり、小さいと丸みがかった形(平たい形)となります。
歪度(わいど)とは、分布の非対称性(左右対称ではない事)を表す指標です。
正規分布は、左右対称なので歪度が0です。
歪度が正(>0)の場合は、左に頂点があり、負の場合は右に頂点がある形となります。
標準得点・偏差値
標準得点とは、集団の中における個人の相対的な位置づけがわかるように変換した値です。
広義には、偏差値も標準得点に含まれるため、ここでは、Z得点と偏差値をまとめます。
Z得点:
Z得点とは、平均が「0」、標準偏差(SD)が「1」となるように変換した得点のことです。
Z得点が「2」の得点をとった人は、「平均+2SD」の位置にいるということを意味します。
Z得点は、データの値から平均値を引き、標準偏差で割ることで計算されます。
[Z得点] = (値 - 平均値) ÷ 標準偏差
偏差値:
偏差値とは、平均が「50」、標準偏差(SD)が「10」となるように変換した得点のことです。T得点とも呼ばれます。
偏差値が「40」の得点をとった人は、「平均-1SD」の位置にいるということを意味します。
偏差値は、Z得点を10倍し50を足すことで計算されます。
[偏差値] = {(値 - 平均値) ÷ 標準偏差 } × 10 + 50
知能検査の結果である、ウェクスラー式の偏差知能指数は、平均を「100」、標準偏差を「15」とした標準得点です。
パーセンタイル値:
パーセンタイル値とは、相対的な位置づけがわかるようにデータを「100」に分けて下から数えた時の順位です。
50パーセンタイル値というと、その値は下から50番目を意味します。
データが、量的な変数(間隔尺度・比例尺度)の場合は、標準得点で相対的な位置づけを表現できます。しかし「順位尺度」の場合は、標準得点を利用できないため、パーセンタイル値を用います。