公認心理師・臨床心理士・心理職(心理系公務員)を目指す方々のための「心理学用語」を説明したサイトです
心理学用語集: 分散分析・カイ2乗検定
6 - 統計・研究法 > 統計 > 16- 分散分析・カイ2乗検定
ここでは、3つの群以上の比較を行う「分散分析」と、質的変数のデータ間の連関(関連性)を検定する「カイ2乗検定」をまとめます。
用語:
- 分散分析 : 要因と水準 / 計画(対応のある・ない・混合) / 主効果・交互作用 / 多重比較
- カイ2乗検定 : 連関 / クロス集計表 / 連関係数・四分点相関係数
分散分析
分散分析とは、「3つ以上」の群や条件のデータの「平均値の差」を分析する方法です。
比較し合う群や条件の「内部のばらつき(分散)」を考慮して、群と群(条件と条件)の間の差(平均値の差)を検定します。
帰無仮説は、比較する群や条件の間の「平均値が等しい」となります。F分布に基づいた「F検定」を利用し、平均値に有意な差がある事(平均値が等しくない事)を検定します。
要因と水準:
要因とは、データに影響を及ぼすと考えられる変数のことです(独立変数)。性別や年齢などです。
水準とは、要因のもつ分類(グループ)のことです。性別ならば、「男」と「女」という2つの水準を持ちます。
例)全国で睡眠時間のアンケートを行い、「年代別」と「都道府県別」に平均値を出したとします。
睡眠時間を分析対象(従属変数)、要因は「年代」、「住居の地域」とします。
年代の水準は、「10代、20代、30代・・・」、地域の水準は、「北海道、東北、甲信越、関東、関西、中国、四国、九州」となります。
分散分析を行うことによって、睡眠時間は、「年代別に差があるか」・「地域別に差があるか」がわかります。
分散分析の計画(対応のある・ない・混合):
分散分析の種類としては、下記が挙げられます(関連:t検定の対応のある・ない)。
- 被験者間計画/分析(独立した群、又は対応のない群):
「複数のグループ間の比較を行うこと」(異なる被検者群の比較)
例)全国から集めた参加者を「年代別」に3群(10代、20代、30代)に分ける。”3群の間”で睡眠時間を「都道府県」を考慮して比較する(平均値の差を分析する)ことは「2要因被験者間分散分析」(2要因とは、年代と都道府県)。 - 被験者内計画/分析(対応のある群):
「同一の被検者内で、複数の条件間の比較を行うこと」
例)参加者の春・夏・秋・冬毎の睡眠時間を集める。同一の被験者において(群は1つ)、睡眠時間を”季節の間”で比較する(平均値の差を分析する)ことは「1要因被験者内分散分析」(1要因は、季節)。 - 混合計画/分析:
「被験者間と被験者内の比較を一緒に行うこと」(被験者間と内が混じり合っている)
例)年代別に3群に分けた参加者の春・夏・秋・冬毎の睡眠時間を集める。”3群の間”で、”各群内”の同一被験者の睡眠時間を季節の違いを考慮して比較する(平均値の差を分析する)ことは「2要因混合分散分析」(2要因は、年代と季節)。
分散分析適用の前提には「等分散性(各水準の母分散がすべて等しいという仮定)」・「正規性(各水準の母手段分布が正規分布しているという仮定)」・「独立性(観測値間が独立していること)」があります。
主効果・交互作用:
まず、主効果とは、ある要因が水準間で平均差を生じさせる効果のことを言います。「主効果がある」とは、その要因の水準間で、分析対象の平均差が有意にあるという事を意味します。
上記の睡眠時間の例で、「10代と20代、20代と30代・・・」といった年代間で差があれば、年代は主効果があるということです。
次に、交互作用とは、「ある要因の水準間の平均値の差が、別の要件の水準によって異なること」を言います。要因の組み合わせによって生じる効果のことです。
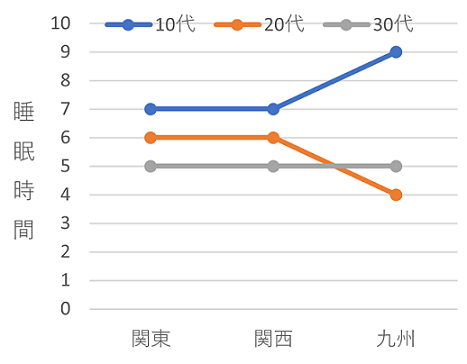
上記の睡眠時間の例で、「年代」の10代と20代を比べると、「地域」が関東・関西の場合は差がないが、九州の場合は大きな差があるといった場合です。
これは、「10代と20代」と「九州」という水準の組み合わせによって違いが生じているので(効果が生じている)、「交互作用がある」ということになります。
交互作業がある場合は、平均値をプロットした図は、プロット線が「交差した図」となります。交互作業がない場合は、プロット線は「並行な図」となります。
多重比較:
分散分析における検定の結果からは、「主効果」と「交互作用」があるかどうかがわかります。
しかし、どの水準間で差があることはわからないので、それを調べるために「多重比較」という方法を用います。
多重比較とは、水準間ごとに平均値の差を比較をおこなうことであり、t検定の拡張とも言えます。しかしt検定は、水準間ごとに”何度”も行うと、第1種の過誤の確率が増えてしまうので、それを補正した方法を行いるのが多重比較です。
多重比較の代表的な方法が、「テューキー法(Tukey)」であり、その他「Fisher法、Bonferroni法、Scheffe法」などがあります。分散分析を行わずとも、多重比較という方法をとれば要因による差があるかどうかはわかりますが(Bonferroni法など)、交互作用を調べるには分散分析という方法が必要となります。
カイ2乗検定
カイ2乗検定は、質的変数(名義尺度)のデータ間に「連関」(関連性)があるかを検定する方法です。
調査の回答が「ある・ない」といった値をとるような場合に、カイ2乗分布を用いて行われる検定方法です。
調査項目となる質的変数は、「有・無(行動など)」、「男・女(性別)」、「賛成・反対(意見)」、「好き、普通、嫌い(好み)」などのカテゴリ(分類)を持ちます。
例)男女合わせて40人に喫煙の有無を調査した結果、
「男で喫煙有:11名」「男で喫煙無し:9名」「女で喫煙有:5名」「女で喫煙無し:15名」でした。
この時に、性別と喫煙の有無に関連性があるかを検定するときに、カイ2乗検定を用います。
「クロス集計表」とは、カテゴリー(分類)に属するデータをそれぞれのカテゴリーで分類し、その度数(データ数)を集計した表のことです。
上記の例(男女合わせて40人に喫煙の有無を調査)のクロス集計表は下記の通りです。
| 喫煙有 | 喫煙無し | 合計 | |
|---|---|---|---|
| 男 | 11 | 9 | 20 |
| 女 | 5 | 15 | 20 |
| 合計 | 16 | 24 | 40 |
この例のように、「有無」の回答が得られ、変数間の関連を調べる場合は「カイ2乗検定」を用いることになります。
連関係数と四分点相関係数:
「クラメールの連関係数」(V)とは、クロス集計表において行と列の変数間(カテゴリ間)の関連性の大きさを表す指標です。「0〜1」の値を取ります。
「四分点相関係数」(φ)とは、「2行×2列」のクロス集計表のみに適用できる、行と列の変数間の相関係数です。「‐1〜+1」の値を取ります。